How Non-Negative Matrix Factorization is Used in Machine Learning?

The data analysis employs various methods and algorithms like Euclidean distance, Gaussian process, etc. Similarly, Non-negative Matrix Factorization (NMF) is also an algorithm that is considered as an alternative approach to decomposition that assumes that the data and the components are non-negative. In this article, we will be discussing Non-Negative Matrix Factorization with its mathematics, implementation, and application in machine learning. The Major points to be discussed in this article are listed below.
Table of Contents
- What is Non-Negative Matrix Factorization (NMF)?
- Mathematics Behind Non-negative Matrix Factorization (NMF)
- Implementation of NMF in Python
- Application of NMF in Machine Learning
What is Non-negative Matrix Factorization (NMF)?
In linear algebra and multivariate analysis, non-negative matrix factorization can be considered as a group of algorithms that are mainly focused on approximating the matrix with non-negative values on it. In this process, any matrix V can be factorized into two matrices W and H.
The above image is a representation of the non-negative matrix factorization of matrix V, where W and H can be multiplied to approximate the matrix V.
The main property of these matrices is that none of the matrices consists of elements greater than zero. Because of the non-negative elements, resultant matrices become easy to inspect. We can find applications of NMF in various fields of machine learning like image processing, text processing, and audio processing. In this article, we will discuss the application of Non-negative Matrix Factorization (NMF) in detail in later sections. Before application, we are required to understand the mathematics behind the Non-negative Matrix Factorization (NMF)
Mathematics Behind Non-negative Matrix Factorization (NMF)
As in the last image, we have seen that, to approximate V, we multiplied the matrix W and H. Let’s consider the below formula.
V = WH
Here the multiplication of the W and H is implemented to compute the V. Multiplication of matrices can also be considered as the linear combination of the column vector W using the coefficient provided by the column of H.
To compute every column of the V, we can use the following formula:
Vi = WHi
Where,
Vi = ith column vector of matrix V,
Hi = ith column vector of the matrix H.
When multiplying matrices, we can see that the dimension of the resultant matrix is much higher than the factor matrices and this causes the NMF to generate factors of any matrix with lower dimensions than the original matrix. For example, V has the dimensions (m x n) and the factors have the dimensions of (m x p) and (p x n), where m and n are significantly higher than the p.
The difference between the dimensions causes NMF to have an inherent clustering property where the column of the resultant matrix is clustered automatically. More formally, when factoring V into W and H, we can obtain minimum error because of the non-negative property.
(|| V – WH ||f) subjected to W?0, H ? 0
After that, applying an orthogonal constraint on H causes the minimization, which is equivalent to the minimization in K-Means clustering.
Here we have seen that having positive elements in the factorization causes the minimization of errors. Now let’s move toward the implementation of NMF in python.
Implementation of NMF in Python
Talking about the implementation of NMF using python, we can use the module provided by the SK-Learn library in the decomposition section. Using the NMF module, we can approximate the non-negative matrix V by multiplying W and H. The objective function is as follows:
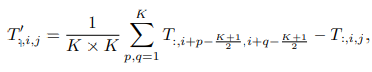
To control the generic norm (|| V – WH ||loss), we can use the beta_loss parameter. Scaling of W and H can be done by n_feature and n_sample parameters, respectively.
In SK-Learn, the NMF module is in the decomposition section which clarifies that it is an approach for dimensionality reduction by assuming data and components are non-negative. We can use this module as an alternative to the PCA module.
Mathematically, using the NFM module by SK-Learn, we can sample matrices that can be decomposed into W and H of non-negative elements. Under the hood of this module, we are optimizing the distance between the X and the product of W and H. One of the majorly used distance functions is the squared Frobenius norm. The formula of the Frobenius norm looks like the following:
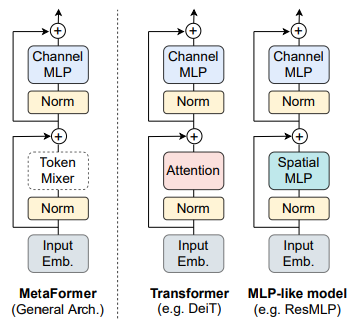
By seeing it, we can say that it is an extension of the euclidean norm for matrices. Let’s take a look at how we can use it for decomposing the face dataset.
Importing libraries:
from numpy.random import RandomState
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces
from sklearn import decompositionLoading the dataset:
faces, _ = fetch_olivetti_faces(return_X_y=True, shuffle=True, random_state=rng)
n_samples, n_features = faces.shapeOutput:
Performing centring:
faces_centered = faces - faces.mean(axis=0)
faces_centered -= faces_centered.mean(axis=1).reshape(n_samples, -1)
print("Dataset consists of %d faces" % n_samples)Output:

Defining variables to represent process log:
import logging
from time import time
logging.basicConfig(level=logging.INFO, format="%(asctime)s %(levelname)s %(message)s")
n_row, n_col = 2, 4
n_components = n_row * n_col
image_shape = (64, 64)
rng = RandomState(0)Plotting the dataset:
plt.figure(figsize=(2.0 * n_col, 2.26 * n_row))
plt.suptitle("First centered Olivetti faces", size=16)
for i, comp in enumerate(faces_centered[:n_components]):
plt.subplot(n_row, n_col, i + 1)
vmax = max(comp.max(), -comp.min())
plt.imshow(
cmap=plt.cm.gray,
interpolation="nearest",
vmin=-vmax,
vmax=vmax,
)
plt.xticks(())
plt.yticks(())
plt.subplots_adjust(0.01, 0.05, 0.99, 0.93, 0.04, 0.0)Output:

Defining estimators:
estimators = [
(
"Eigenfaces - PCA",
decomposition.PCA(
n_components=n_components, svd_solver="randomized", whiten=True
),
True,
),
(
"Non-negative components - NMF",
decomposition.NMF(n_components=n_components, init="nndsvda", tol=5e-3),
False,
),
]Here we are going to see a comparison between PCA and NMF. We have defined two estimators from the decomposition module of SK-Learn.
Applying estimators to the dataset:
for name, estimator, center in estimators:
print("Extracting the top %d %s..." % (n_components, name))
t0 = time()
data = faces
if center:
data = faces_centered
estimator.fit(data)
train_time = time() - t0
print("done in %0.3fs" % train_time)
if hasattr(estimator, “cluster_centers_”):
components_ = estimator.cluster_centers_
else:
components_ = estimator.components_
# Plot an image representing the pixelwise variance provided by the
# estimator e.g its noise_variance_ attribute. The Eigenfaces estimator,
# via the PCA decomposition, also provides a scalar noise_variance_
# (the mean of pixelwise variance) that cannot be displayed as an image
# so we skip it.
if (
hasattr(estimator, “noise_variance_”) and estimator.noise_variance_.ndim > 0
): # Skip the Eigenfaces case
plot_gallery(
“Pixelwise variance”,
estimator.noise_variance_.reshape(1, -1),
n_col=1,
n_row=1,
)
plot_gallery(
“%s – Train time %.1fs” % (name, train_time), components_[:n_components]
)
plt.show()
Output:
Here we have seen how we can use the NMF on python for decomposing data. Now, let’s move towards the application of NMF in machine learning.
Application of NMF in Machine Learning
In the above section, we have discussed details of non-negative matrix factorization like how it works and how we can implement it using python. In this section, we are discussing the sections of machine learning where we can use the NMF. Since in the implementation, we have seen how we can use it with images, it will be a good step to start with understanding the application of NMF in image processing.
Image processing: In the implementation, we have seen that we can use NFM for decomposing the data wherein the data we have 400 samples of face images. Behind the code, the process we followed is that we start with loading the greyscale images and the image contains pixels in matrix format. Using the NMF, we produced factorized matrices W and H and to approximate the real images we multiplied W and H and found the estimated images of the faces.
Here, we can say that the NFM can be used in various processes of image processing where we are required to decompose images or we are required to estimate new images. By clustering the image’s pixels, we can also make many things like a colour analyzer, colour separator, etc, and also it can be used in various fields like Bioinformatics and Nuclear imaging.
Text processing: When we talk about the data in a text process, it is one kind of sequential data and many procedures in text processing use the representation of the data in the form of a document term matrix. In a document term matrix, we convert the data into a matrix form and again using the NMF, we can produce W and H from the matrix.
The columns of W can be interpreted as basis documents (bags of words) and H tells us how to sum contributions from different words to reconstruct the documents. Using the NFM, we can complete the text classification task, where identifying and reconstruction can be completed by the NFM.
Data Imputation: In machine learning, data is one of the major factors on which any process depends. It becomes very necessary in the process to provide quality data to the algorithm to extract a quality result from the algorithm. In such a scenario we find that the problem of data missing is very normal and frequently occurring. Using the NMF, we can take the missing values while minimizing its cost function. Unlike other methods which treat the missing value as zero, NMF proves that the missing values in the data are ignored in the cost function.
The process of data imputation using the NMF can be completed in two major steps:
- Prove the effect of the missing values during the data imputation have the level of the second order. At this stage, we are familiar with the components of NMF.
- Prove that impact from missing data during component construction is a first-to-second order effect.
Audio processing: In the audio processing, we see there are two types of noises in signal: one is stationary and another one is non-stationary noise. So there are various methods available to deal with the stationary noises and when it comes to a signal with non-stationary noise, we can use the NMF for denoising the signal from nonstationary noise. The basic algorithm for this has the following steps:
- Train Two models: One for main audio and one for noise and whenever noisy audio is given, the noise can be separated using the NMF.
- Models trained on the main audio can be used for estimating the separated audio.
Mainly in audio processing, we find the application of NMF in speech recognition for denoising non-stationary speech.
Final Words
In the article, we have discussed the non-negative matrix factorization with the mathematics behind it. We have also discussed the implementation using the python programming language and Scikit-Learn library. Along with this, we discussed the application of NMF in the field of machine learning.



